Vừa qua Trung tâm gia sư Thanh niên cũng đã truyền tải cho các em thấy được những nội dung cốt lõi của chương trình lớp 7. Và nội dung tiếp theo mà trung tâm sẽ cung cấp cho các em là chương trình lớp 8 bên dưới đây.

I/ PHẦN ĐẠI SỐ

1/ Nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức ta nhân đơn thức với từng số hạng của đa thức rồi cộng các tích lại với nhau

Công thức minh họa: A.(B+C) = A.B + B.C

VD: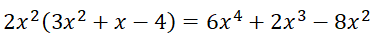

2/ Nhân đa thức với đa thức

Muốn nhân một đa thức với một đa thức ta nhân mỗi hạng tử của đa thức này với từng số hạng của đa thức kia rồi cộng các tích lại với nhau

Công thức minh họa: (A+B).(C+D) = A.C + A.D + B.C + B.D

VD:

3/ Bảy hằng đẳng thức đáng nhớ

Cách học dễ nhớ 7 hàng đẳng thức đáng nhớ:

• a sẽ là bậc cao nhất, b là bậc thấp nhất. Rồi từ trái qua phải bậc của a sẽ giảm dần về 0 còn b thì ngược lại.
• Phương pháp ghi nhớ bằng hình ảnh
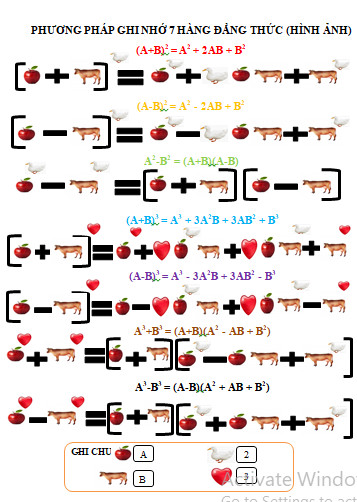
• Phương pháp ghi nhớ bằng câu chuyện

4/ Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Phân tích đa thức thành nhân tử là biến đổi đa thức đó thành một tích của những đa thức

VD:

5/ Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

VD: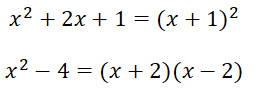

6/ Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử

VD:

• •     3x² – 3xy + x – y
  • = (3x² – 3xy) + (x – y)
  • = 3x(x – y) + (x – y)
  • = (x – y)(3x – 1)

7/ Phân tích đa thức thành nhân tử bằng phương pháp phối hợp nhiều phương pháp

Phương pháp này đòi hỏi các em phải có nguyên tắc để nhận dạng và phân tích phương pháp để áp dụng. Một số nguyên tắc để áp dụng dạng này như sau:

• Quan sát các đơn thức trong đa thức xem có chỗ nào giống về số hoặc biến không, nếu có thì rút nhân tử ra, còn không thì xem nó có thuộc hằng đẳng thức nào không. Nếu không nữa thì tiến hành nhóm hạng tử.

VD1: 10x²y + 5x – 15xy²

• Đối với bài này ta quan sát về phần số ta có: 10 ; 5 ; 15. Thì ta thấy các số này đều chia hết cho 5. Vậy giống nhau con số 5
• Đối với phần chữ ta có: x²y ; x ; xy² Thì ta thấy giống nhay ở biến x
• Vậy ta sử dụng phương pháp đặt nhân tử chung.

Giải: 10x²y + 5x – 15xy² = 5x(xy + 1 – 3y²)

VD2: x² – 2xy + y² – 9

• Đối với bài này thì ta thấy phần số và phần biến không giống nhau hoàn toàn nên ta không sử dụng phương pháp đặt nhân tử được, ta tiến hành phương pháp hằng đẳng thức. Ta thấy có 3 hạng tử nhóm lại thành hằng đẳng thức số 2. Xong ra thấy được hằng đẳng thức số 3.

Giải:

• • (x² – 2xy + y² ) – 9
  • = (x – y)²– 3²
  • = (x – y – 3)(x – y + 3)

8/ Phép cộng các phân thức đại số

Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức

VD: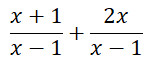

Giải: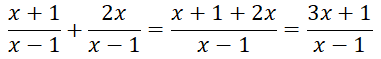

Muốn cộng hai đa thức khác mẫu, ta quy đồng mẫu thức rồi cộng tử thức lại với nhau

VD: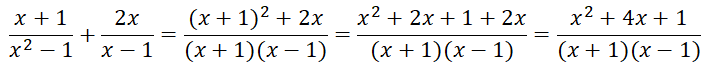

II/ PHẦN HÌNH HỌC

Các em phần học dấu hiệu nhận biết của hình thang, hình thang cân, hình bình hành, hình chữ nhật, hình vuông, hình thoi