Đầu tiên cần nắm những kiến thức cơ bản của chương trình học kì 2 lớp 9. Những nội dung cơ bản cần nắm:
1/ Cần nắm được điều kiện xác định khi giải phương trình chứa biến:
– Trường hợp 1: Biểu thức chứa biến ở mẫu số phải khác không
-
vd:

– Trường hợp 2: Biểu thức chứa biến nằm trong dấu căn ở tử số phải lớn hơn bằng không
- vd:
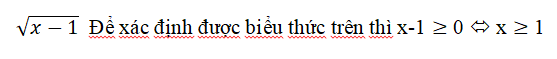
– Trường hợp 3: Biểu thức chứa biến nằm trong dấu căn ở mẫu số phải lớn hơn không
- vd:
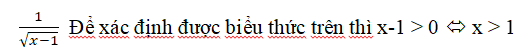
2/ Cần nắm được 7 hàng đẳng thức đáng nhớ:

3/ Cần nắm được phương pháp giải hệ phương trình bằng phương pháp cộng đại số
4/ Cần nắm được phương pháp giải phương trình bậc 2 bằng denta, tính nhanh denta, hệ thức vi-et
5/ Cần nắm được các dạng giải tham số m và phương pháp giải của các dạng đó:
Các dạng giải tham số m
1/ Dạng 1:
- Tìm m để phương trình có 2 nghiệm phân biệt
- Tìm m để phương trình có nghiệm kép
- Tìm m để phương trình vô nghiệm
- Tìm m để phương trình có nghiệm
2/ Dạng 2:
- Chứng minh m để phương trình có 2 nghiệm phân biệt
- Chứng minh m để phương trình có nghiệm
3/ Dạng 3:
- Tìm m để phương trình trên thỏa mãn 1 phương trình nào đó
4/ Dạng 4:
- Tìm m để phương trình có 2 nghiệm trái dấu
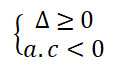
- Tìm m để phương trình có 2 nghiệm cùng dấu
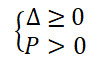
- Tìm m để phương trình có 2 nghiệm cùng âm
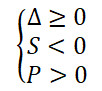
- Tìm m để phương trình có 2 nghiệm cùng dương
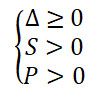
Phương pháp giải:
1/ Dạng 1:
- Tìm m để phương trình có 2 nghiệm phân biệt:
– Giải denta có tham số m
– Để phương trình có 2 nghiệm phân biệt thì denta lớn hơn 0 từ đó ta tìm được m
- Tìm m để phương trình có nghiệm kép
– Giải denta có tham số m
– Để phương trình có 2 nghiệm phân biệt thì denta bằng 0 từ đó ta tìm được m
- Tìm m để phương trình vô nghiệm
– Giải denta có tham số m
– Để phương trình có 2 nghiệm phân biệt thì denta bé hơn 0 từ đó ta tìm được m
- Tìm m để phương trình có nghiệm
– Giải denta có tham số m
– Để phương trình có 2 nghiệm phân biệt thì denta lớn hơn bằng 0 từ đó ta tìm được m
2/ Dạng 2:
- Chứng minh m để phương trình có 2 nghiệm phân biệt
– Giải denta có tham số m
– Ta đưa tham số m vào 1 bình phương để thỏa điều kiện bình phương luôn lớn hơn bằng 0 và cộng thêm 1 số dương để cho ta thấy được denta luôn lớn hơn 0 với mọi m tìm được
- Chứng minh m để phương trình có nghiệm
– Giải denta có tham số m
– Ta đưa tham số m vào 1 bình phương để thỏa điều kiện bình phương luôn lớn hơn bằng 0 để cho ta thấy được denta luôn lớn hơn bằng 0 với mọi m tìm được
3/ Dạng 3:
- Giải denta để tìm điều kiện của tham số m luôn có 2 nghiệm phân biệt. Denta lớn hơn 0
- Áp dụng hệ thức vi-et để tìm tổng tích
- Đưa phương trình đã cho về dạng tổng tích, xong thế hệ thức vi-et vào, rồi ta giải denta tìm tham số m
4/ Dạng 4:
- Giải denta để tìm điều kiện của tham số m luôn có 2 nghiệm phân biệt. Denta lớn hơn bằng 0
- Áp dụng hệ thức vi-et để tìm tổng tích
- Thế vào công thức phù hợp theo từng yêu cầu của đề bài (công thức đã nêu ở trên).

